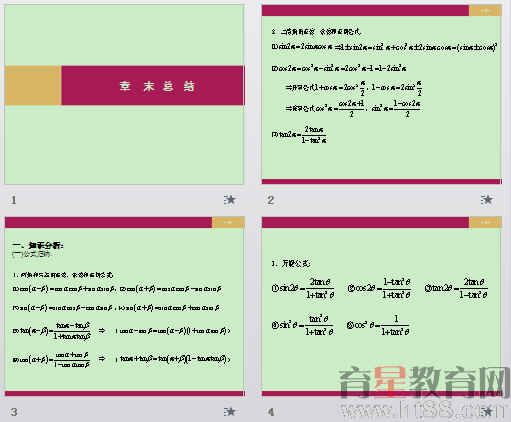
2015秋高中数学（课件+教学设计）必修四第三章　三角恒等变换（13份）
　　3.1.1  两角差的余弦公式.pptx
　　3.1.1  两角差的余弦公式学案教学设计（二）课件.pptx
　　3.1.1学案设计.docx
　　3.1.2 两角和与差的正弦、余弦、正切公式.pptx
　　3.1.2学案设计.docx
　　3.1.3   二倍角的正弦、余弦和正切公式.pptx
　　3.1.3学案设计.docx
　　3.2  简单的三角恒等变换(第二课时).pptx
　　3.2  简单的三角恒等变换(第一课时).pptx
　　3.2.1学案设计.docx
　　3.2.2学案设计.docx
　　3.3学案设计.docx
　　《三角恒等变换》章末总结.pptx

　　第三章　函数的应用
　　3.1　函数与方程
　　3.1.1　方程的根与函数的零点
　　学习目标
　　①明确“方程的根”与“函数的零点”的密切联系,学会结合函数图象性质判断方程根的个数及多种方法求方程的根和函数的零点;
　　②通过本节学习让学生掌握“由特殊到一般”的认知规律,在今后学习中利用这一规律探索更多的未知世界;
　　③通过本节学习不仅让学生学会数学知识和认知规律,还要让学生充分体验“数学语言”的严谨性,“数学思想方法”的科学性,体会这些给他们带来的快乐.
　　合作学习
　　一、设计问题,创设情境
　　问题1:求下列方程的根.
　　(1)6x-1=0;
　　(2)3x2+6x-1=0;
　　(3)3x5+6x-1=0.(如何解,会解吗?)
　　问题2:求下面方程的实数根.
　　lnx+2x-6=0.
　　问题3:怎么解一般方程f(x)=0?
　　问题4:方程f(x)=0的根与函数y=f(x)之间有什么样的关系呢?
　　二、学生探索,尝试解决
　　活动1:请同学们先观察几个具体的一元二次方程及其相应的二次函数
　　①方程x2-2x-3=0的解为　　　　,函数y=x2-2x-3的图象与x轴有　　　　个交点,坐标为　　　　. 
　　②方程x2-2x+1=0的解为　　　　,函数y=x2-2x+1的图象与x轴有　　　　个交点,坐标为　　　　. 
　　③方程x2-2x+3=0的解为　　　　,函数y=x2-2x+3的图象与x轴有　　　　个交点,坐标为　　　　. 
　　根据以上观察结果,可以得到:
　　结论:一元二次方程的根就是相应的二次函数图象与x轴交点的　　　　.若一元二次方程无实数根,则相应的二次函数图象与x轴无交点. 
　　反思:函数y=f(x)的零点、方程f(x)=0的实数根、函数y=f(x)的图象与x轴交点的横坐标,三者有什么关系?
　　活动2:所有函数都存在零点吗?什么条件下才能确定零点的存在呢?
　　画出函数f(x)=x2-2x-3的图象,
　　1.在区间[-2,1]上有零点,计算f(-2)=　　　　,f(1)=　　　　,发现f(-2)·f(1)　　　　(选填“<”或“>”)0. 
　　2.在区间[2,4]上是否也具有这种特点呢?
　　……
　　第三章　三角恒等变换
　　3.1　两角和与差的正弦、余弦和正切公式
　　3.1.3　二倍角的正弦、余弦、正切公式
　　学习目标
　　以两角和的正弦、余弦和正切公式为基础,推导二倍角的正弦、余弦和正切公式,理解推导过程,掌握其应用.
　　合作学习
　　一、复习回顾,承上启下
　　复习:
　　cos(α-β)=　　　　　　; 
　　cos(α+β)=　　　　　　; 
　　sin(α-β)=　　　　　　; 
　　sin(α+β)=　　　　　　; 
　　tan(α+β)=　　　　　　; 
　　tan(α-β)=　　　　　　. 
　　练习:
　　(1)在△ABC中,sin Asin B<cos Acos B,则△ABC为(　　)
　　A.直角三角形 B.钝角三角形
　　C.锐角三角形 D.等腰三角形
　　(2)cos-sin的值为(　　)
　　A.0 B.2
　　C. D.-
　　思考:已知<β<α<,cos(α-β)=,sin(α+β)=-.求sin 2α.我们由此能否得到sin 2α,cos 2α,tan 2α的公式呢?
　　二、学生探索,揭示规律
　　1.sin 2α=2sin αcos α.
　　2.cos 2α=cos2α-sin2α=　　　　=　　　　. 
　　变式:
　　……
　　第三章　函数的应用
　　3.2　函数模型及其应用
　　3.2.2　函数模型的应用实例
　　学习目标
　　①了解函数拟合的基本思想,学会建立拟合函数模型解决实际问题;
　　②借助信息技术,利用数据画出函数图象,从拟合简单的一次函数模型入手,掌握多角度观察函数图象的技能,探究出各种合适的拟合函数模型.在建构知识的过程中体会数形结合的思想与从特殊到一般的归纳思想;
　　③体验探究的乐趣,了解函数是描述变化规律的基本数学模型,培养学生分析、解决问题的能力.
　　合作学习
　　一、设计问题,创设情境
　　大家已看到在课本第三章的章头图中,说的是有名的“澳大利亚的人兔大战”.859年,有人从欧洲带进澳洲几只兔子,由于澳洲有茂盛的牧草,而且没有兔子的天敌,兔子数量不断增加,到1890年,新南威尔士州的兔子数量据估计就有3600万只.到1926年,全澳洲的兔子数量已经增长到了创纪录的100亿只.可爱的兔子变得可恶起来,100亿只兔子吃掉了相当于10亿只羊所吃的牧草,草原的载畜率大大降低,而牛、羊是澳大利亚的主要牲口.这使澳大利亚人头痛不已,他们采用各种方法消灭这些兔子,直至二十世纪五十年代,科学家采用载液瘤病毒杀死了百分之九十的野兔,澳大利亚人才算松了一口气.
　　与之相应,图中话道出了其中的意蕴:对于一个种群的数量,如果在理想状态(如没有天敌、食物充足等)下,那么它将呈指数增长;但在有限制的环境中,种群数量一般符合对数增长模型.
　　前面我们学习过两种函数模型的应用,分别是利用给定函数模型解决实际问题、建立确定性的函数模型解决问题,那么在既没有给出函数模型又无法建立确定性函数模型的情况下,又该如何解决实际问题呢?
　　二、自主探索,尝试解决
　　问题1:一辆汽车在某段路程中的行驶速率与时间的关系如图所示.
　　(1)求图中阴影部分的面积,并说明所求面积的实际含义;
　　(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004km,试建立行驶这段路程时汽车里程表读数s km与时间t h的函数解析式,并作出相应的图象.
　　再次探索:
　　(1)将图中的阴影部分隐去,得到的图象有什么意义?