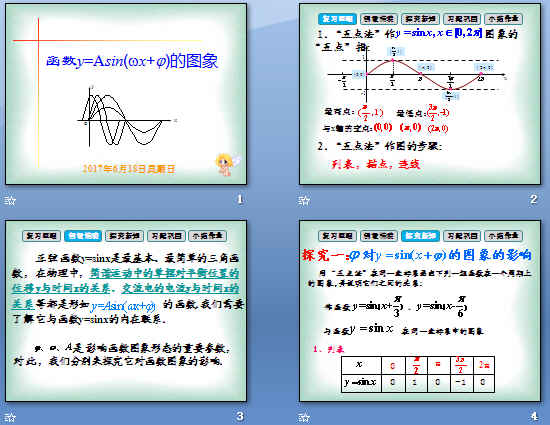
必修四1.5函数yAsin ωx+φ的图象教学课件共28张PPT含说课稿+教学设计+教案定案+初案 （5份打包）
1.5函数y=Asin(ωx+φ)的图象 初案.doc
1.5函数y=Asin(ωx+φ)的图象 定案.doc
1.5函数y=Asin(ωx+φ)的图象 教学设计.doc
1.5函数y=Asin(ωx+φ)的图象 说课稿.doc
1.5函数y=sin(wx+t)的图象.ppt
共28张。数形结合分析，探究归纳性质，适合新课教学。

　　1.5函数y=Asin(ωx+)(A>0，ω>0)的图象 （定案）
　　城南中学 周克传
　　上课时间：2017年4月12日上午第四节
　　授课班级：高一（3）班
　　一、教学目标：
　　1、知识与技能
　　1. 对y = sin(x+)的图像的影响。
　　2. ω对y = sin(ωx+)的图像的影响。
　　3. A对y = Asin(ωx+)的图像的影响。
　　2、过程与方法
　　会用相位变换、周期变换、振幅变换分别作y = sin(x+)、y = sin(ωx+)、y = Asin(ωx+)的图像。
　　3、情感态度价值观
　　1.渗透数形结合思想、增强作图能力;了解由简单到复杂，由特殊到一般的化归思想；培养全面分析、抽象和概括的能力。
　　2. 培养动与静的辩证关系，善于从运动的观点观察问题，并解决问题。
　　二、教学重点、难点
　　1、教学重点：将参数A，ω，对函数y = Asin(ωx+)图象的影响的问题进行分解，从而学习如何将一个复杂问题分解为若干个简单问题的方法。
　　2、教学难点：ω对函数y = Asin(ωx+)的图象的影响规律的概括
　　3、教学关键：理解三个参数A、ω、φ对函数y = Asin(ωx+)（ω＞0，A＞0）图像的影响。
　　三、教学过程：
　　一、导入新课，提出课题
　　师：正弦函数y=sinx是最基本、最简单的三角函数，在物理中，简谐运动中的单摆对平衡位置的位移y与时间x的关系、交流电的电流y与时间x的关系等都是形如y = Asin(ωx+j)的函数.我们需要了解它与函数y=sinx的内在联系
　　揭示课题：函数y = Asin(ωx+j)的图像（一）（板书）
　　二、推进新课
　　师： 要研究这个函数跟正弦函数的关系，那我们看这个解析式y = Asin(ωx+j)，它分别有三个参数，一个是A，一个是ω，还有一个是j，那如果以此式研究它的话，有点困难，并且难以看出这三个参数的影响，因此我们一个一个去研究它。
　　探究一：参数j对y = sin(x+j)的图像的影响
　　1、用五点作图法在同一个坐标系里，作出函数y = sinx和y = sin(x+ )的函数图像，并比较这两个函数图像的关系
　　教师引导学生从图像直接看出来只要将y= sinx的图像向左平移 个单位便得到函数y = sin(x+ )的图像。
　　1.5函数y=Asin(ωx+)(A>0，ω>0)的图象 说课稿
　　城南中学 周克传
　　上课时间：2017年4月12日上午第四节
　　授课班级：高一（3）班
　　一、教学分析
　　本节通过图象变换,揭示参数φ、ω、A变化时对函数图象的形状和位置的影响,讨论函数y=Asin(ωx+φ)的图象与正弦曲线的关系,以及A、ω、φ的物理意义,并通过图象的变化过程,进一步理解正、余弦函数的性质,它是研究函数图象变换的一个延伸,也是研究函数性质的一个直观反映.这节是本章的一个难点.
　　如何经过变换由正弦函数y=sinx来获取函数y=Asin(ωx+φ)的图象呢?通过引导学生对函数y＝sinx到y＝Asin(ωx+φ)的图象变换规律的探索,让学生体会到由简单到复杂、由特殊到一般的化归思想；并通过对周期变换、相位变换先后顺序调整后,将影响图象变换这一难点的突破,让学生学会抓住问题的主要矛盾来解决问题的基本思想方法;通过对参数φ、ω、A的分类讨论,让学生深刻认识图象变换与函数解析式变换的内在联系.
　　本节课建议充分利用多媒体,倡导学生自主探究,在教师的引导下,通过图象变换和“五点”作图法,正确找出函数y＝sinx到y＝Asin(ωx+φ)的图象变换规律,这也是本节课的重点所在.
　　一、教学目标：
　　1、知识与技能
　　1. 对y = sin(x+)的图像的影响。
　　2. ω对y = sin(ωx+)的图像的影响。
　　3. A对y = Asin(ωx+)的图像的影响。
　　2、过程与方法
　　会用相位变换、周期变换、振幅变换分别作y = sin(x+)、y = sin(ωx+)、y = Asin(ωx+)的图像。
　　3、情感态度价值观
　　1.渗透数形结合思想、增强作图能力;了解由简单到复杂，由特殊到一般的化归思想；培养全面分析、抽象和概括的能力。
　　2. 培养动与静的辩证关系，善于从运动的观点观察问题，并解决问题。
　　二、教学重点、难点
　　1、教学重点：将参数A，ω，对函数y = Asin(ωx+)图象的影响的问题进行分解，从而学习如何将一个复杂问题分解为若干个简单问题的方法。
　　2、教学难点：ω对函数y = Asin(ωx+)的图象的影响规律的概括
　　3、教学关键：理解三个参数A、ω、φ对函数y = Asin(ωx+)（ω＞0，A＞0）图像的影响。
　　三、教学过程：
　　一、导入新课，提出课题
　　师：正弦函数y=sinx是最基本、最简单的三角函数，在物理中，简谐运动中的单摆对平衡位置的位移y与时间x的关系、交流电的电流y与时间x的关系等都是形如y = Asin(ωx+j)的函数.我们需要了解它与函数y=sinx的内在联系
　　揭示课题：函数y = Asin(ωx+j)的图像（一）（板书）
　　二、推进新课
　　师： 要研究这个函数跟正弦函数的关系，那我们看这个解析式y = Asin(ωx+j)，它分别有三个参数，一个是A，一个是ω，还有一个是j，那如果以此式研究它的话，有点困难，并且难以看出这三个参数的影响，因此我们一个一个去研究它。