选修2-1第二章《圆锥曲线与方程》复习课课件(12张ppt)+知识点总结+训练题+几何画板等素材共5份(5份打包)
2.3.2.双曲线的简单几何性质.gsp
椭圆焦点三角形问题.jpg
圆锥曲线复习训练题.doc
圆锥曲线与方程复习.ppt
圆锥曲线知识点总结.doc
圆锥曲线知识总结
一、知识点总结
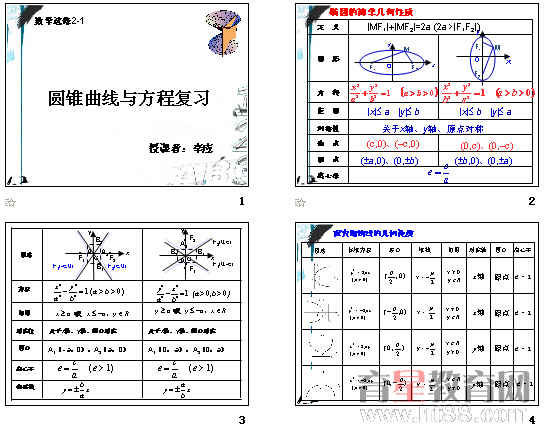
椭圆知识点总结
定义 第一定义: ;
第二定义: .
标准
方程 焦点在 轴上:
焦点在 轴上 :
焦点
顶点 焦点在 轴上: ,
焦点在 轴上: ,
范围 ,
,
离心率
准线 焦点在 轴上:
焦点在 轴上:
关系 的关系:
焦点
三角形面积 若 是椭圆 上一点, 、 是其两个焦点,且 ,则 的面积 .(焦点三角形的面积公式由余弦定理和椭圆(或双曲线)的定义推导可得.)
备注 1. 当焦点位置不确定时:椭圆的方程可以统一设为 ,避免分类讨论的麻烦;
2. 具有相同焦点的椭圆和双曲线的方程:与椭圆 具有相同焦点的椭圆 的方程可设为 .
弦长公式 ( 为交点 所在直线的方程)
双曲线知识点总结
定义 第一定义: ;
第二定义: .
标准
方程 焦点在 轴上:
焦点在 轴上:
焦点
顶点 焦点在 轴上: ,
焦点在 轴上: ,
范围 或 ;
或 ;
渐近线 焦点在 轴上:
焦点在 轴上:
离心率
准线 焦点在 轴上:
焦点在 轴上:
关系 的关系:
焦点
三角形面积 若 是双曲线 上一点, 、 是其两个焦点,且 ,则 的面积 .(焦点三角形面积公式由余弦定理和椭圆(或双曲线)定义推导可得.)
圆锥曲线复习训练题
班别: 姓名: 学号:
一、选择题:
1.双曲线2x2-y2=8的实轴长是 ( ).
A.2 B.22 C.4 D.42
2.如果方程x2+ky2=2表示焦点在y轴上的椭圆,那么实数k的取值范围是( )
A.(1,+∞) B.(1,2) C.(12,1) D.(0,1)
3.已知椭圆与双曲线x23-y22=1有共同的焦点,且离心率为15,则椭圆的标准方程为 ( ).
A.x220+y225=1 B.x225+y220=1 C.x225+y25=1 D.x25+y225=1
4.若椭圆 上的点到直线y=x+m的最短距离是 ,则m最小值为( ).
A.-1 B. C. D.1
5.设 是椭圆 的两个焦点, 是椭圆上的点,且 ,则 的面积为( )
A.4 B.6 C. D.
6.已知椭圆x2a2+y2b2=1(a>b>0)与双曲线x2m2-y2n2=1(m>0,n>0)有相同的焦点(-c,0)和(c,0),若c是a、m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率是( )
A.33 B.22 C.14 D.12
7.动圆的圆心在抛物线y2=8x上,且动圆恒与直线x+2=0相切,则动圆必过点( )
A.(4,0) B.(2,0) C.(0,2) D.(0,-2)
二、填空题





资源评论
共有 0位用户发表了评论 查看完整内容我要评价此资源