2016版《步步高》高考数学大二轮总复习与增分策略(全国通用,文科)配套课件+配套文档:专题五 立体几何(4份打包)
2016版《步步高》高考数学大二轮总复习与增分策略(全国通用,文科)配套课件+配套文档:专题五 立体几何 第1讲.docx
2016版《步步高》高考数学大二轮总复习与增分策略(全国通用,文科)配套课件+配套文档:专题五 立体几何 第1讲.pptx
2016版《步步高》高考数学大二轮总复习与增分策略(全国通用,文科)配套课件+配套文档:专题五 立体几何 第2讲.docx
2016版《步步高》高考数学大二轮总复习与增分策略(全国通用,文科)配套课件+配套文档:专题五 立体几何 第2讲.pptx
第1讲 空间几何体
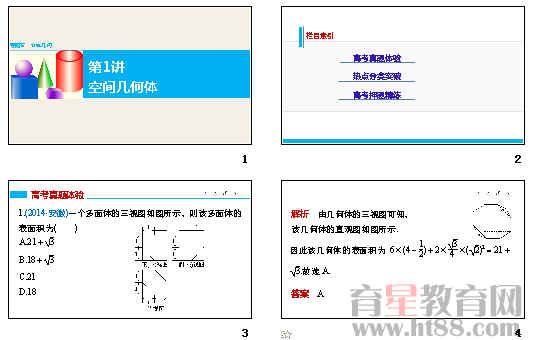
1.(2014•安徽)一个多面体的三视图如图所示,则该多面体的表面积为( )
A.21+3 B.18+3
C.21 D.18
2.(2015•山东)在梯形ABCD中,∠ABC=π2,AD∥BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )
A.2π3 B.4π3 C.5π3 D.2π
3.(2014•湖北)《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:置如其周,令相乘也.又以高乘之,三十六成一.该术相当于给出了由圆锥的底面周长L与高h,计算其体积V的近似公式V≈136L2h.它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式V≈275L2h相当于将圆锥体积公式中的π近似取为( )
A.227 B.258
C.15750 D.355113
4.(2014•江苏)设甲,乙两个圆柱的底面积分别为S1,S2,体积分别为V1,V2.若它们的侧面积相等,且S1S2=94,则V1V2的值是________.
1.以三视图为载体,考查空间几何体面积、体积的计算.2.考查空间几何体的侧面展开图及简单的组合体问题.
热点一 三视图与直观图
1.一个物体的三视图的排列规则
俯视图放在正(主)视图的下面,长度与正(主)视图的长度一样,侧(左)视图放在正(主)视图的右面,高度与正(主)视图的高度一样,宽度与俯视图的宽度一样.即“长对正、高平齐、宽相等”.
2.由三视图还原几何体的步骤
一般先从俯视图确定底面再利用正视图与侧视图确定几何体.
例1 (1)(2014•课标全国Ⅰ)如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是( )
A.三棱锥 B.三棱柱
C.四棱锥 D.四棱柱
(2)一几何体的直观图如图,下列给出的四个俯视图中正确的是( )
思维升华 空间几何体的三视图是从空间几何体的正面、左面、上面用平行投影的方法得到的三个平面投影图,因此在分析空间几何体的三视图问题时,先根据俯视图确定几何体的底面,然后根据正视图或侧视图确定几何体的侧棱与侧面的特征,调整实线和虚线所对应的棱、面的位置,再确定几何体的形状,即可得到结果.
跟踪演练1 (1)一个几何体的三视图如图所示,则该几何体的直观图可以是( )
(2)将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为( )
热点二 几何体的表面积与体积
空间几何体的表面积和体积计算是高考中常见的一个考点,解决这类问题,首先要熟练掌握各类空间几何体的表面积和体积计算公式,其次要掌握一定的技巧,如把不规则几何体分割成几个规则几何体的技巧,把一个空间几何体纳入一个更大的几何体中的补形技巧.
例2 (1)(2015•北京)某三棱锥的三视图如图所示,则该三棱锥的表面积是( )
A.2+5 B.4+5
C.2+25 D.5
(2)如图,在棱长为6的正方体ABCD-A1B1C1D1中,E,F分别在C1D1与C1B1上,且C1E=4,C1F=3,连接EF,FB,DE,BD则几何体EFC1-DBC的体积为( )
A.66 B.68
C.70 D.72
思维升华 (1)求多面体的表面积的基本方法就是逐个计算各个面的面积,然后求和.(2)求体积时可以把空间几何体进行分解,把复杂的空间几何体的体积分解为一些简单几何体体积的和或差.求解时注意不要多算也不要少算.
跟踪演练2 (2015•四川)在三棱柱ABCA1B1C1中,∠BAC=90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边的长为1的等腰直角三角形,设点M,N,P分别是AB,BC,B1C1的中点,则三棱锥PA1MN的体积是________.
热点三 多面体与球
与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.
例3 (1)已知三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=23,AB=1,AC=2,∠BAC=60°,则球O的表面积为( )
A.4π B.12π C.16π D.64π
(2)(2015•课标全国Ⅱ)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥OABC体积的最大值为36,则球O的表面积为( )
A.36π B.64π C.144π D.256π
思维升华 三棱锥P-ABC可通过补形为长方体求解外接球问题的两种情形:





资源评论
共有 0位用户发表了评论 查看完整内容我要评价此资源