必修四《1.4.1正弦函数、余弦函数的图象》课件(9张ppt)+教学设计+随堂练习(3份打包)
1.4.1正弦函数、余弦函数的图象 9张ppt.ppt
1.4.1正弦函数、余弦函数的图象 教学设计.doc
1.4.1正弦函数、余弦函数的图象 随堂练习.doc
课题 1.4.1 正弦函数、余弦函数的图象教学设计
教
学
目
标 知识与技能 了解利用单位圆中的正弦线画正弦曲线的方法
过程与方法 掌握“五点法”画正弦曲线和余弦曲线的步骤和方法,能用“五点法”作出简单的正、余弦曲线.
情感态度价值观 研究函数的性质常常以图象直观为基础,通过观察函数的图象,从图象的特征获得函数的性质是一个基本方法.
重点 能用“五点法”作出简单的正、余弦曲线.
难点 “五点法”作图的基本步骤和要领要熟练掌握.
教
学
设
计 教学内容 教学环节与活动设计
探究点一 几何法作正弦曲线
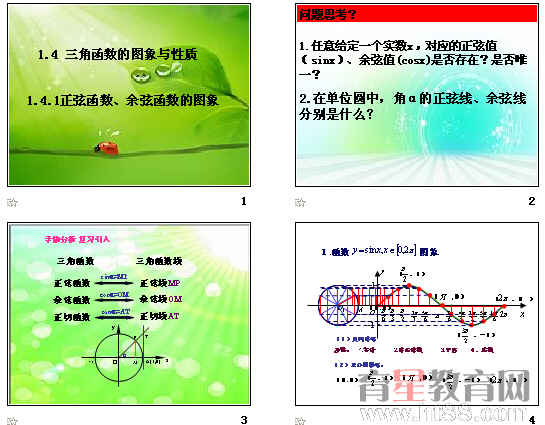
利用几何法作正弦函数y=sin x,x∈[0,2π]的图象的过程如下:
①作直角坐标系,并在直角坐标系y轴的左侧画单位圆,如图所示.
②把单位圆分成12等份(等份越多,画出的图象越精确).过单位圆上的各分点作 的垂线,可以得到对应于0,π6,π3,π2,…,2π等角的正弦线.
③找横坐标:把x轴上 (2π≈6.28)这一段分成12等份.
④找纵坐标:将 线对应平移,即可得到相应点的纵坐标.
⑤连线:用平滑的曲线将这些点依次从左到右连接起来,即得y=sin x,x∈[0,2π]的图象.
因为终边相同的角有相同的三角函数值,所以函数y=sin x,x∈[2kπ,2(k+1)π),k∈Z且k≠0的图象,与函数y=sin x,x∈[0,2π)的图象的形状完全一致.于是我们只要将函数y=sin x,x∈[0,2π)的图象向左、向右平行移动(每次2π个单位长度),就可以得到正弦函数y=sin x,x∈R的图象. 教师讲解单位圆中的正弦线作正弦函数图像的方法。应注意引导学生思考如何得到图像上的一个点?
让学生思考单位圆中的圆心角与数轴上的点对应,可以把相应的正弦线平移到相应的位置吗?
为什么要把单位圆分成12等分?





资源评论
共有 0位用户发表了评论 查看完整内容我要评价此资源