2015年10月深圳市教师技能大赛人教版必修一1.3《函数的基本性质——单调性》课件(13张ppt)+教学设计+几何画板素材共3份
函数的单调性(许美玲).doc
函数的单调性(许美玲)1.ppt
未命名1.gsp
§1.3.1函数的单调性
深圳第二外国语学校 许美玲
一、教学内容分析:
本节选自人教版《高中课程标准实验教科书》A版必修1第一章第三节。在此之前,学生已学习了函数的概念、定义域、值域及表示法,这为过渡到本节的学习起着铺垫作用。本节内容是高中数学中相当重要的一个基础知识点,是研究和讨论初等函数有关性质的基础。掌握本节内容不仅为今后的函数学习打下理论基础,还有利于培养学生的抽象思维能力及分析问题和解决问题的能力。
二、学情分析:
从学生的知识上看,学生已经学过一次函数,二次函数,反比例函数等简单函数,函数的概念及函数的表示,接下来的任务是对函数应该继续研究什么.从各种函数关系中研究它们的共同属性,应该是顺理成章的。
从学生现有的学习能力看,通过初中对函数的认识与实验,学生已具备了一定的观察事物的能力,积累了一些研究问题的经验,在一定程度上具备了抽象、概括的能力和语言转换能力。
我校学生基础较弱,学生头脑中虽有一些函数性质的实物实例,但并没有上升为“概念”的水平,如何给函数性质以数学描述?如何“定性”“定量”地描述函数性质是学生关注的问题,也是学习的重点问题。函数的单调性是学生从已经学习的函数中比较容易发现的一个性质,学生也容易产生共鸣,通过对比产生顿悟,渴望获得这种学习的积极心向是学生学好本节课的情感基础。
三、教学目标:
1.知识与技能:理解函数单调性的定义,判断及证明;
2.过程与方法:通过函数单调性定义的形成,培养学生观察、归纳、抽象的能力,渗透数形结合的思想;
3.情感态度价值观:通过形式化与符号化对函数单调性的描述,促使学生养成用运动、发展、变化的观点认识世界的思维习惯.
四、教学重点与难点:
1.教学重点:函数单调性的定义;
2.教学难点:归纳抽象出函数的单调性的定义,根据定义证明函数的单调性.
五、教法学法
1.借助多媒体和几何画板软件
2.以教师启发讲授为主,学生自主探究为辅的教学模式
六、教学过程设计:
(一)创设情境,引入新课:
前面,我们学习了有关函数的基本概念,下面通过函数的图象来研究函数的性质。
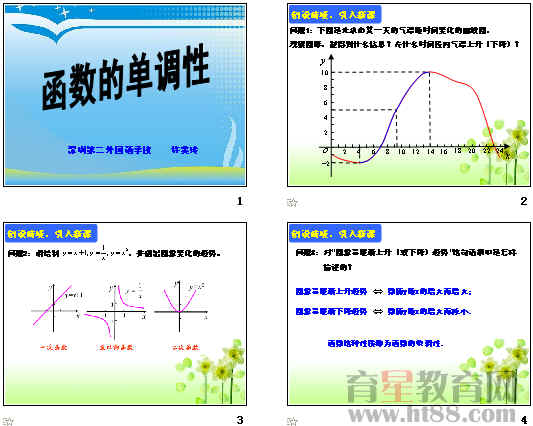
问题1:下图是北京市某一天的气温随时间变化的曲线图,观察图形,能得到什么信息?
学生可能回答:最高最低气温何时达到及温度的变化.
生活中,我们关系很多数据的变化,比如水位高低、股票价格等等,用函数的观点看,其实就是函数值在随着自变量的变化。
【设计意图】由生活情境引入新课,激发兴趣.
(二)借助图像,直观感知
问题:2:请绘制 ,并指出图象变化的趋势。
观察得到:随着x值的增大,函数图象有的呈上升趋势,有的呈下降趋势,有的在一个区间内呈上升趋势,在另一区间内呈下降趋势。
问题3:对“图象呈逐渐上升(或下降)趋势”这句话初中是怎样描述的?
回顾初中对函数单调性的解释:
图象呈逐渐上升趋势 数值y随x的增大而增大;
图象呈逐渐下降趋势 数值y随x的增大而减小。
函数这种性质称为函数的单调性。
【设计意图】学生在函数单调性这一概念的学习上有三个认知基础:一是函数图象,二是初中对函数单调性的认识。对照绘制的函数图象,让学生回忆初中对函数单调性的描述的定义,并在此基础上进行概念的符号化建构,与学生的认知起点衔接紧密,符合学生的认知规律。
问题4:(1)右图是函数y=f(x)的图像,它的单调性是怎样的呢?
(先展示图像,再给出解析式f(x)=0.001x+1)





资源评论
共有 0位用户发表了评论 查看完整内容我要评价此资源