《平面向量数量积的物理背景及其含义》ppt9
- 资源简介:
平面向量数量积的物理背景及其含义
2.4.1 平面向量数量积的物理背景及其含义 (1).doc
2.4.1 平面向量数量积的物理背景及其含义 (1).ppt
2.4.1 平面向量数量积的物理背景及其含义 (2).doc
2.4.1 平面向量数量积的物理背景及其含义 (2).ppt
2.4.1 平面向量数量积的物理背景及其含义 (3).doc
2.4.1 平面向量数量积的物理背景及其含义 (3).ppt
2.4.1 平面向量数量积的物理背景及其含义.doc
2.4.1 平面向量数量积的物理背景及其含义.ppt
人教版全日制高中《数学》必修四P103—105
2.4.1平面向量数量积的物理背景及其含义
东莞市麻涌中学 陈楚芳
一、教材分析
平面向量的数量积是在学习了向量的相关概念,以及向量的加法、减法、实数与向量的积之后,高中数学的又一重要概念和运算.数量积的概念以及数量积的几何意义是本节课的重点,既是学习数量积性质和运算律的前提,也为今后利用数量积处理有关模长、角度、垂直等问题奠定了基础.
二、学情分析
基础知识方面:学生之前学习了向量的相关概念、向量的线性运算以及平面向量基本定理等内容,同时学生对平面向量数量积的物理背景(如功、力的分解等)有一定的了解,这些都为概念的理解作好了必要的铺垫.
认知水平与能力方面:学生已经具备初步的抽象概括能力,能在教师的引导下,通过自主学习、合作交流解决一些实际问题.
任教班级学情:我班学生是体育生,基础一般,但思维比较活跃,而对于概念的深入理解和灵活运用的能力还有待进一步提高,须逐步引导.
三、目标分析
依据教学大纲的要求和新课程教学理念,结合本节课的特点和学生的实际情况,本节课的教学目标确定为:
1、知识目标
(1)理解两非零向量的夹角的概念,掌握平面向量的数量积及其几何意义;
(2)能初步运用数量积的相关概念和运算律进行运算.
2、能力目标
经历向量的数量积、投影等概念的形成过程,提高类比辨析、抽象概括等数学思维能力.
3、情感目标
教学活动过程中,始终贯穿了对平面向量数量积的物理背景的深入挖
……
《平面向量数量积》测试题
1. △ABC中, =a, =b,则 等于 ( )
A.a+b B.-(a+b) C.a-b D.b-a
2.已知|p|= ,|q|=3, p与q的夹角为 ,则以a=5p+2q,b=p-3q为邻边的平行四边形的一条对角线长为 ( )
A.15 B. C. 16 D.14
3.设e1,e2是夹角为450的两个单位向量,且a=e1+2e2,b=2e1+e2,则|a+b|的值 ( )
A. B.9 C. D.
4.若|a|=1,|b|= ,(a-b)⊥a,则a与b的夹角为 ( )
A.300 B.450 C.600 D.750
5.在△ABC中, =c, = a, =b,则下列推导中错误的是 ( )
A.若a•b<0,则△ABC为钝角三角形 B. 若a•b=0,则△ABC为直角三角形
C. 若a•b=b•c,则△ABC为等腰三角形 D. 若c•( a+b+c)=0,则△ABC为等腰三角形
二、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中的横线上)
6.在△ABC中,已知 且 则这个三角形的形状是 .
7.给出下列命题:①若a2+b2=0,则a=b=0;
③已知a,b,c是三个非零向量,若a+b=0,则|a•c|=|b•c|
……
福建师大二附中2013—2014学年第二学期区级教学开放周教案
平面向量数量积的物理背景及其含义
学科:数学 班级:高一7班 教师:江薇
研究方向:在学生自学的基础上,提高课堂学习的效率
教学目标:
1、知识与能力:掌握数量积的定义,性质、运算律。
2、过程与方法:遵循数量积的知识的拓展过程进行教学,是学生能更深刻的体会到知识的发展与变化。
3、情感、态度、价值观:在整个学校过程中体会知识的发展变化,同时也伴随着思维的变化,感受变化,产生对学习的兴趣,体会数学的价值。
教学重点:平面向量的数量积定义,性质
教学难点:平面向量数量积的定义及运算律的理解和平面向量数量积的应用
教学过程:
问题1:我们已经学习了向量的哪些运算?这些运算的结果是什么?
我们说生活中存在既有方向,又有大小的量,比如物理中的力,力的合成又给了我们启示,归纳得出向量和的平行四边形法则,所以数学是源自于生活的,数学又是从生活中抽象出来的,因此数学又是高于生活的。
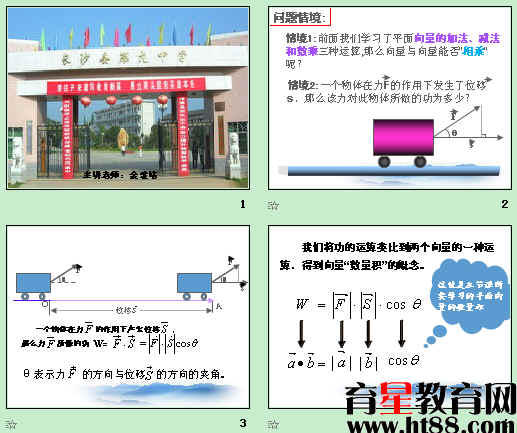
问题2:生活中还有这样一种情况:
如图所示,一物体在力F的作用下产生位移S ,
(1)力F所做的功W= 。
把式子写成 ,它的意义就看的更清楚了,表示力F在运动方向上的分力 在运动方向上的做功。
(2) 请同学们分析这个公式的特点?
W(功)是 量,F(力)是 量, S(位移)是 量, θ是 。
两个矢量参与的运算,结果却是标量,这就是我们今天要学习的向量的一个新运算的一个模型,这个新的运算就是向量的数量积。
定义:两个非零向量, , ,我们把数量 叫作 , 的数量积(或内积),




资源评论
共有 0位用户发表了评论 查看完整内容我要评价此资源