2015年10月深圳市教学技能大赛人教版必修一1.3《函数的基本性质_单调性》课件(15张ppt)+教案共2份
单调性(讲课教案).doc
单调性(讲课课件).ppt
课题:§1.3.1函数的单调性
一、 教材分析:
本节课是人教版数学必修1第一章《集合与函数概念》§1.3.1函数的基本性质的第一课时,该课时主要学习增函数、减函数的定义,以及应用定义解决一些简单问题。函数的性质是研究函数的基石,函数的单调性是学生在了解函数概念后学习的函数的第一个性质,也是函数学习中第一个用数学符号语言刻画的概念,为进一步学习函数其他性质提供了方法依据。因此函数的单调性既是学生学过的函数概念的延续和拓展,又是后续研究指数函数、对数函数、三角函数的单调性的基础。此外在比较数的大小、函数的定性分析以及相关的数学综合问题中也有广泛的应用,它是整个高中数学中起着承上启下作用的核心知识之一。
二、 学情分析:
教学对象是刚进入高中的学生,虽然具有一定的分析问题和解决问题的能力,逻辑思维能力也初步形成,但由于年龄的原因,思维尽管活跃、敏捷,却缺乏冷静、深刻,因而片面、不够严谨。同时学生的认知困难主要在两个方面:
(1)用准确的数学符号语言刻画图象的上升与下降,这种由形到数的翻译,从直观到抽象的转变对高一的学生是比较困难的;
(2)单调性的证明是学生在函数内容中首次接触到的代数论证内容,而学生在代数方面的推理论证能力是比较薄弱的。
三、 教学目标:
知识与技能:使学生理解函数单调性的概念,掌握判别函数单调性的方法;
过程与方法:从实际生活问题出发,引导学生自主探索函数单调性的概念,应用图象和单调性的定义解决函数单调性问题,让学生领会数形结合的数学思想方法,培养学生发现问题、分析问题、解决问题的能力;
情感态度价值观:让学生体验数学的科学功能、符号功能和工具功能,培养学生直觉观察、探索发现、科学论证的良好的数学思维品质。
四、 教法与学法
1、教法分析
(1)通过学生熟悉的实际生活问题引入课题,为概念学习创设情境,拉近数学与现实的距离,激发学生求知欲,调动学生主体参与的积极性。
(2)在运用定义解题的过程中,紧扣定义中的关键语句,通过学生的主体参与,逐个完成对各个难点的突破,以获得各类问题的解决。
(3)在鼓励学生主体参与的同时,不可忽视教师的主导作用.具体体现在设问、讲评和规范书写等方面,要教会学生清晰的思维、严谨的推理,并成功地完成书面表达。
(4)采用投影仪、多媒体等现代教学手段,增大教学容量和直观性。
2、学法分析
(1)让学生从问题中质疑、尝试、归纳、总结、运用,培养学生发现问题、研究问题
和解决问题的能力。
(2)让学生利用图形直观启迪思维,并通过正、反例的构造,来完成从感性认识到理性思维的一个飞跃
五、 教学重难点
1、教学重点
函数单调性的概念,并运用函数单调性的定义判断、证明一些函数的单调性。
2、教学难点
形成增(减)函数概念的过程中,如何从图像升降的直观认识过渡到函数增减的数学符号语言表述,用定义证明函数的单调性。
七、教学过程:
(一).情景引入:
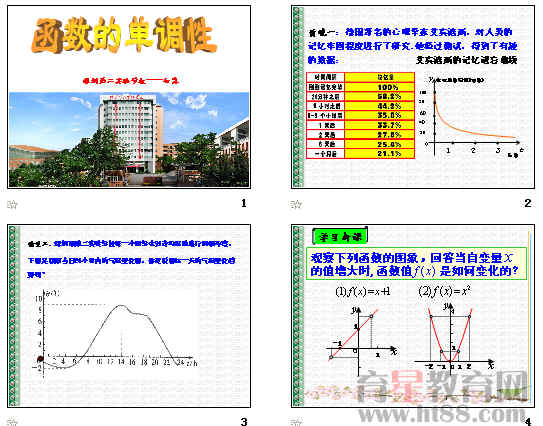
1.情景一:德国著名心理学家艾宾浩斯的研究数据:
时间间隔 记忆保持量
刚刚记忆完毕 100%
20分钟之后 58.2%
1小时之后 44.2%
8-9小时之后 35.8%
1天后 33.7%
2天后 27.8%
6天后 25.4%
一个月后 21.1%
… …
将表中数据绘制在坐标系中连出草图,这就是著名的艾宾浩斯记忆遗忘曲线. 观察这条曲线,你能得出什么规律呢?由这个规律我们如何去高效学习?(学生回答)
这是一条衰减曲线,随着时间的推移,记忆的保持量逐渐减小。第一天遗忘的速度最快,一天之后遗忘的速度趋于缓慢。这一规律就提醒我们:在学习新知识的时候,一定要及时进行复习和巩固,以便加深理解和记忆。
2、情景二:一日气温变化图





资源评论
共有 0位用户发表了评论 查看完整内容我要评价此资源