必修一:3.1.1方程的根与函数的零点(课件,教案,练习等9份打包)(
~$设计(刘彩艳).doc
方程的根与函数的零点2015.5.19.ppt
观课记录(刘彩艳).doc
教材分析(刘彩艳).doc
教学设计(刘彩艳).doc
课标分析(刘彩艳).doc
课后反思(刘彩艳).doc
评测练习(刘彩艳).doc
效果分析(刘彩艳).doc
学情分析(刘彩艳).doc
《方程的根与函数的零点》教学设计
【环节一:巧设疑云,轻松渗透】设置问题情境,渗透数学思想
教师活动:请同学们思考这个问题。解方程:
(1) ;(2) .(3) ;(4) .
学生活动:回答,思考解法。
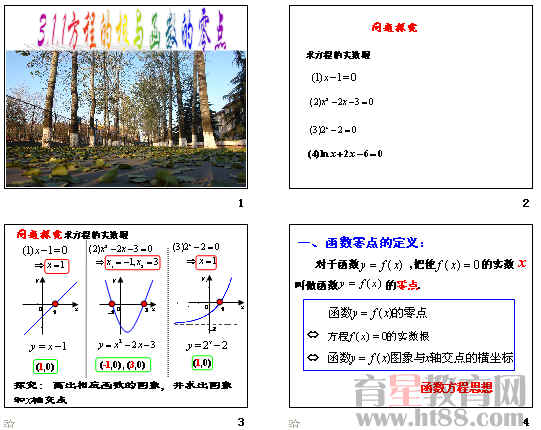
教师活动:第四个方程我们没有学过它的解法,通过这节课的学习我们来解决这个问题。上一章我们学习了基本初等函数,这节课我们就通过研究函数来解决方程根的问题。画出前三个方程相应函数的图象,并求出图象和x轴交点.
学生活动:动手画图并求解。
教师活动:用屏幕显示方程的根、函数的图象以及函数图象与x轴交点的坐标。观察三者之间的关系。
学生活动:观察图象,思考作答。得到方程的实数根是函数图象与x轴交点的横坐标,是使函数值为零的x的结论。
教师活动:我们就把使f(x)=0的实数x称做函数的零点.
设计意图:通过纯粹靠代数运算无法解决的方程,引起学生认知冲突,激起探求的热情.
通过回顾一次函数、二次函数、指数函数图象与x轴的交点和相应方程的根的关系,将结论推广到一般函数,为零点概念做好铺垫.
【环节二:形成概念,升华认知】引入零点定义,确认等价关系
教师活动:这是我们本节课的第一个知识点。板书函数零点的定义。
教师活动:结合函数零点的定义和我们刚才的探究过程,你认为方程的根与函数的零点究竟是什





资源评论
共有 0位用户发表了评论 查看完整内容我要评价此资源