《函数的单调性》ppt60(3份)
- 资源简介:
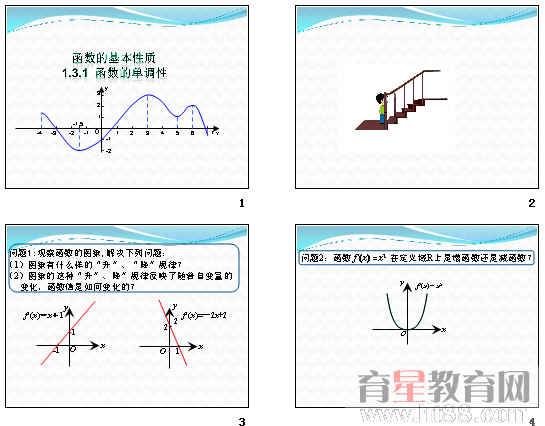
共18张。问题探究,图文结合,适合新课教学。
全国第八届青年数学教师优质课展示课件与教学设计—函数的单调性与最值(湖南省常德市汉寿县第一中学 李婷婷)
函数的单调性教学设计(李婷婷).doc
课件.ppt
《1.3.1单调性与最大(小)值第1课时》教学设计
湖南省常德市汉寿县第一中学 李婷婷
课型:新授课
一、教学内容解析
《函数的单调性》是《高中数学人教 A 版》(必修 1)第一章 1.3.1 节的内容,本节课的主要内容是从形与数两方面理解函数单调性的概念,依据图象判断函数的单调性和应用定义证明一些简单函数在给定区间上的单调性.
函数的单调性是学生在了解函数概念之后学习的第一个函数性质,也是函数学习中第一个用数学符号语言刻画的性质.函数单调性的研究体现了对函数研究的一般方法.这就是:加强数形的结合,由直观到抽象,由特殊到一般.即借助对函数图象的观察、分析、归纳,发现函数增、减变化的直观特征,进一步量化,发现增、减变化的数字特征,从而加以解析研究,用准确的数学语言刻画.函数的单调性为研究函数的其他性质起到了示范作用,提供了方法依据.
函数的单调性有着承前启后的作用.一方面,函数的单调性是前一节内容函数的概念与图象知识的延续与扩展,同时函数的单调性又是后续研究指数函数、对数函数、幂函数及其他函数单调性的理论基础,在解决函数定义域、值域、不等式、比较两数大小等具体问题中均有着广泛的应用;此外,从方法论的角度分析,本节教学过程当中,还渗透了数形结合、归纳类比、转化与化归等数学思想.利用定义证明函数单调性的过程中,算法的思想提前渗透,在强调对单调性概念中的“任意”理解的同时,为后面逻辑用语中的全称量词和存在性量词的深入理解提前做了铺垫.
本节课的教学重点:形成增(减)函数的形式化定义.
二、教学目标设置
根据新课标的要求和教学内容的结构特征,依据学生学习认知的心理规律和素质教育的要求,并结合本校学生的实际水平,确定本节课教学目标如下:
1.从形与数两方面理解函数单调性的概念,会根据函数图象判断函数的单调性,指出函数的单调区间;
2.能够根据函数单调性的定义证明函数在指定区间上的单调性;
3.通过对函数单调性定义的探究,渗透数形结合的思想方法,培养学生观察、归纳、抽象的能力和语言表达能力;通过对函数单调性的证明,提高学生的推理论证能力;在经历观察发现、抽象概括,自主建构单调性概念的过程中,让学生体会从具体到抽象,从特殊到一般,从感性到理性的认知过程.
目标解析:
1.在探究函数单调性定义时,领悟到数形结合思想、归纳类比思想、转化与化归思想,并能运用这些数学思想观察、分析函数的图象,探究、归纳、概括出函数单调性的概念.
2.能够以具体的例子说明函数在某区间上是增函数还是减函数;能够举例,并通过绘制图象说明函数在定义域的某区间上具有单调性,而在整个定义域上未必具有单调性,说明函数的单调性是函数的局部性质.对于一个简单函数能够用单调性的定义证明它在指定区间上是增函数还是减函数.
三、学生学情分析
从学生的知识上看,学生已经学过一次函数、二次函数及反比例函数、函数的概念及表示,能画出一些简单函数的图象,从图象的直观变化,学生能粗略的领会函数增减性的概念,从而引入函数单调性的定义也就水到渠成.
从学生现有的学习能力来看,通过初中对函数的认识和实验,学生已具备一定的观察事物的能力,积累了一些研究问题的经验,在一定程度上具备了抽象、概括的能力和语言转换能力.
从学生的学习心理上看,学生头脑中虽有一些函数性质的实物实例,但并没有上升为“概念”的水平,如何“定性”“定量”的描述函数性质是学生关注的问题,也是学习的重难点问题.函数的单调性是学生从已经学习的函数中比较容易发现的一个性质,学生渴望进一步学习,这种积极心态是学生学好本节课的情感基础.但是如何运用数学符号将自然语言的描述转化为形式化的定义,学生接受起来还比较困难.在教学中要多引导,让学生真正的理解函数单调性的定义.




资源评论
共有 0位用户发表了评论 查看完整内容我要评价此资源