广东省广州市第一中学人教版数学选修1-1：3.3导数在研究函数中的应用（学案+课件，8份）（
　　文数导学案65（3.3.1函数的单调性与导数(一)）.doc
　　文数导学案65（3.3.1函数的单调性与导数（一）.ppt
　　文数导学案66（3.3.1函数的单调性与导数(二)）.doc
　　文数导学案66（3.3.1函数的单调性与导数（二））.ppt
　　文数导学案67（函数的极值与导数）.doc
　　文数导学案67（函数的极值与导数）课件.ppt
　　文数导学案68（3.3.3函数的极值与导数）.doc
　　文数导学案68（3.3.3函数的极值与导数）课件.ppt
　　3.3.1  函数的单调性与导数(一)
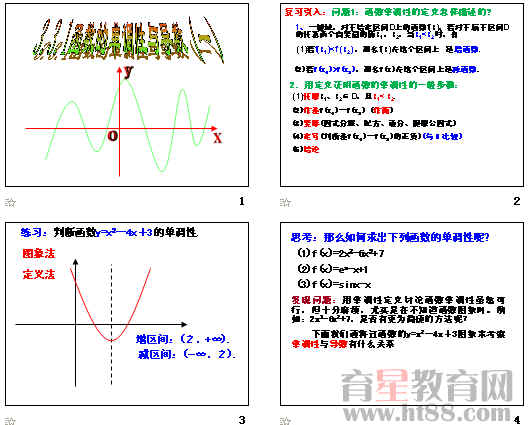
　　【课前导学】  1、判断函数的单调性有哪些方法？判断y=x2-4x+3的单调性，并指出其单调区间？
　　思考：如果遇到函数：y=2x3-6x2+7判断单调性呢？还有其他方法吗？
　　2、【探究1】 观察下面函数的图象，并探讨函数的单调性与其导数正负的关系
　　函数 定义域 导数 增区间 增区间上导数的正负 减区间 减区间上导数的正负
　　4、函数的单调性与导数的关系:    在某个区间 内，如果 ，那么函数 在这个区间内        ；如果 ，那么函数 在这个区间内         。
　　特别的，如果 ，那么函数 在这个区间内是        ．
　　【预习自测】   1、（1）函数 的减区间是                      ；
　　（2）函数 的增区间是              ；减区间是   
　　3.3.2函数的极值与导数
　　【学习目标】
　　1．了解函数在某点取得极值的必要条件和充分条件．
　　2．会用导数求函数的极大值、极小值(其中多项式函数一般不超过三次)．
　　【课前导学】
　　1．极值点与极值
　　如图，若函数y＝f(x)在点x＝a的函数值f(a)比它在点x＝a附近其他点的函数值都小，f′(a)＝0，而且在点x＝a附近的左侧                  ，右侧                   ，则把点a叫做函数y＝f(x)的极小值点，f(a)叫做函数y＝f(x)的极小值．
　　如图，函数y＝f(x)在点x＝b的函数值f(b)比它在点x＝b附近其他点的函数值都大，f′(b)＝0，而且在点x＝b附近的左侧              ，右侧                ，则把点b叫做函数y＝f(x)的               ，f(b)叫做函数y＝f(x)的              ，极小值点、极大值点统称为                ，极大值和极小值统称为                ．
　　2．求函数f(x)极值的方法
　　3.3.3函数的最值与导数
　　【学习目标】
　　1．能够区分极值与最值两个不同的概念．
　　2．会求闭区间上函数的最大值、最小值(其中多项式函数一般不超过三次)．
　　【课前导学】
　　1. 观察右边一个定义在区间[a,b]上的函数y=f(x)的图象.
　　发现图中____________是极小值，_________是极大值，
　　在区间上的函数的最大值是______，最小值是_______。
　　2．求函数y＝f(x)在[a，b]上的最值的步骤
　　(1)求函数y＝f(x)在(a，b)内的               ；
　　(2)将函数y＝f(x)的                与                                f(a)，f(b)比较，其中最大的一个是最大值，最小的一个是最小值．
　　【预习自测】
　　1．下列说法正确的是(    )
　　(A)函数的极大值就是函数的最大值
　　(B)函数的极小值就是函数的最小值
　　(C)函数的最值一定是极值       
　　(D)若函数的最值在区间内部取得,则一定是极值.
　　2.函数y=f(x)在区间［a,b］上的最大值是M，最小值是m,若M=m,则 (   )
　　(A)等于0 (B)大于0   (C)小于0 (D)以上都有可能
　　3.函数y= ,在［－1,1］上的最小值为(  )
　　(A)0 (B)－2    (C)－1 (D)