共15张，有教案及说课稿。
　　一次函数与一元一次不等式
　　翠微中学   罗 琦
　　教学目标：
　　知识与技能目标：认识一次函数与一元一次不等式之间的关系，学会用图象的方法表示不等式及解集。
　　过程与方法目标：体会数形结合的思想。
　　情感态度目标：  学生通过自己探究，相互交流，培养学生积极思考，团结协作的精神和自主学习的习惯。培养学生数形结合的思想。
　　教学重点：理解一次函数与一元一次不等式的关系，会用图象表示不等式的解集。
　　教学难点：数形结合的思想，尤其2方面：
　　1.ax+b>0(a,b是常数, a≠0)对应的图象与x轴的位置关系。
　　2.a1x+b1＞a2x+b2(a1,a2≠0,a1,a2,b1,b2是常数)对应的图象，直线a1x+b1与直线a2x+b2的位置关系。
　　教学过程： 
　　创设情境，建立模型：
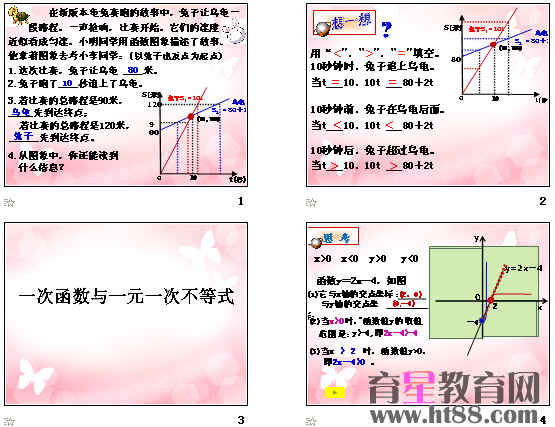
　　在新版本龟兔赛跑的故事中，兔子让乌龟一段路程。一声枪响，比赛开始。它们的速度近似看成匀速。小明同学用函数图象描述了故事。他拿着图象去考小李同学：(以兔子出发点为起点) 
　　1.这次比赛，兔子让乌龟     米。
　　2.兔子跑了    秒追上了乌龟。
　　3.若比赛的总路程是90米，       先到达终点；若比赛的总路程是120米，
　　先到达终点。
　　4.从图象中，你还能读到什么信息？
　　（比如兔子和乌龟的速度，10秒前（后）兔子在乌龟前面（后面）等。）
　　5.用数学式子表示其中的几条信息
　　（用“<”，“>”，“=”填空）。
　　(1)10秒钟时，兔子追上乌龟。
　　当t   10，10t    80＋2t
　　(2)10秒钟前，兔子在乌龟后面。
　　当t   10，10t    80＋2t
　　(3)10秒钟后，兔子超过乌龟。
　　当t   10，10t    80＋2t
　　（前4问，利用课件，引导学生从图象中看出数据信息。第5问，引导学生观察不等关系，在图象中对应的位置。）
　　新课探究，解释模型：
　　模型一：ax+b>0(a,b是常数, a≠0)对应的图象与x轴的位置关系：在上方。
　　【思 考】:
　　1.x>0、x<0、y>0、y<0在平面直角坐标系中图象在哪一区域？
　　（利用课件，显示结果）
　　2.函数y＝2x－4，如图（右）
　　(1)它与x轴的交点坐标：          ;
　　与y轴的交点坐标：