华师大版九年级上册22.3实践与探索同步备课资料
华师大版九年级上册22.3实践与探索教案.doc
华师大版九年级上册22.3实践与探索(1).ppt
华师大版九年级上册22.3实践与探索(2).ppt
华师大版九年级上册22.3实践与探索教案(2).doc
华师大版九年级上册22.3实践与探索练习题(有答案).doc
华师大版九年级上册22.3实践与探索教案(1)
教学内容:课本P38页~P40页。
教学目标:
1、通过具体的实例,建立起用一元二次方程解决实际问题的方法体系;
2、利用平移改变图形的组合方式,从而突出本质特性;
3、形成率类问题的解题经验;
教学重点:应用题的分析方法;
教学难点:找等量关系;
教学准备:课件
教学方法:讲授法
一、练习
1、不解方程,求下列方程的两根之和与两根之积;
(1)(x+1)(x-2)=2 (2) 3x2+7x=6
2、已知方程3x2-5x+m=0的一个根是 ,求方程的另一个根和m的值。
二、学习
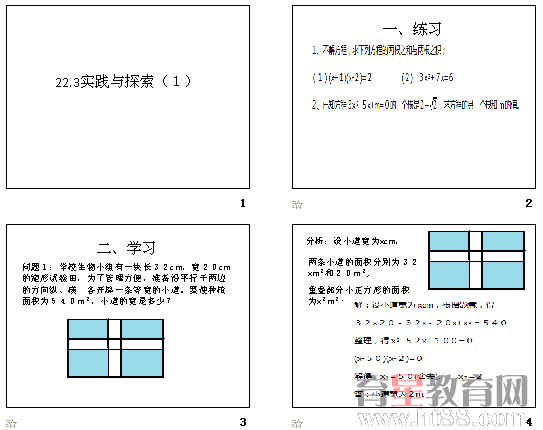
1、学习问题1:学校生物小组有一块长32cm,宽20cm的矩形试验田,为了管理方便,准备沿平行于两边的方向纵、横 各开辟一条等宽的小道。要使种植面积为540m2,小道的宽是多少?
分析:设小道宽为xcm,则两条小道的面积分别为32xm2和20m2,其中重叠部分小正方形的面积为x2m2.
解:设小道宽为xcm,根据题意,得
32×20-32x-20x+x2=540
整理,得x2-52x+100=0
(x-50)(x-2)=0
解得:x1=50(舍去), x2=2
答:小道宽为2m。
如果设想把小道平移到两边,如图所示,小道所占面积不变。种植面积就是一个矩形,矩形的长为(32-x)m,宽为(20-x)m,于是可以列出方程:
(32-x)(20-x)=540
2、学习问题2:某药品经过两次降价,每瓶零售价由56元降为31.5元。已知两次降价的百分率相同,求每次降价的百分率。
分析:设每次降价的百分率为x,则第一次降价后的价格为56(1-x),第二次降价后的价格为56(1-x)(1-x)=56(1-x)2;
解:设每次降价的百分率为x,根据题意,得
56(1-x)2=31.5
解这个方程,得
x1=0.25, x2=1.75.
因为降价的百分率不可能大于1,所以x2=1.75不符合题意。经检验,x=0.25=25%符合题要求。
答:每次降价的百分率为25%。
3、例1、(2016重庆B卷)近期猪肉价格不断走高,引起了民众与政府的高度关注.当市场猪肉的平均价格每千克达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.
(1)从今年年初至5月20日,猪肉价格不断走高,5月20日比年初价格上涨了60%.某市民在今年5月20日购买2.5千克猪肉至少要花100元钱,那么今年年初猪肉的最低价格为每千克多少元?
华师大版九年级上册22.3实践与探索教案(2)
教学内容:课本P40页~P43页。
教学目标:
1、通过具体的实例,体验用一元二次方程解决实际问题的方法;
2、通过变式寻找问题的本质;
3、形成图形问题的解题经验;
教学重点:应用题的分析方法;
教学难点:找等量关系;
教学准备:课件
教学方法:讲授法
教学过程
一、 练习
课本P43第5、6题
二、学习
1、学习问题3:小明把一张边长为10cm的正方形硬纸板的四周各剪去一个同样大小的正方形,再折叠成一个无盖的长方体盒子,如图所示。
(1) 如果要求长方体的底面积为81cm2,那么剪去的正方形边长为多少?
(2) 如果按下表列出的长方体底面积的数据要求,那么剪去的正方形边长会发生怎样的变化?折叠成的长方体的侧面积又会发生怎样的变化?
折叠成的长方体底面积(cm2) 81 64 49 36 25 16 9 4
剪去的正方形边长(cm)
折叠成的长方体侧面积cm2)
分析:设剪去的正方形的边长为xcm,则长方体的底面正方形的边长为(10-2x)cm。长方体的底面积为(10-2x)2cm2;长方体的侧面积为4块相同的长方形,其长为(10-2x)cm,宽为xcm,侧面积为4x(10-2x)cm2.
解:(1)设剪去的正方形的边长为xcm,根据题意,得





资源评论
共有 0位用户发表了评论 查看完整内容我要评价此资源